「08」贪心 2

相关题目

例1. 国王游戏

例2. Cow Acrobats

Cow Acrobats

$n$ 个元素，第 $i$ 个元素有值为 $w_i$ 和 $s_i$ 的两个属性，定义风险值 $f_i$ 为前 $i - 1$ 个元素的 $w$ 值之和减去 $s_i$。现问 $n$ 个元素如何排列，可使得所有的风险值的最大值极可能的小。

注意到交换元素 $k$ 和 $k + 1$ 的位置，不影响其他元素的风险值。因此，我们考虑如何调整 $k$ 和 $k + 1$ 的顺序，结果更优。

调整之前：

$f_k = \sum_{i = 1}^{k - 1}w_i - s_k$, $f_{k + 1} = \sum_{i=1}^kw_i-s_{k+1}$

调整之后：

$F_k= \sum_{i = 1}^{k - 1}w_i + w_{k + 1} - s_k$, $F_{k + 1} = \sum_{i=1}^kw_i - w_k-s_{k+1}$

现在，我们要比较的是 $\max \{ f_k, f_{k+1} \}$， $\max \{ F_k, F_{k+1} \}$ 的大小关系。

注意到这 $4$ 项均含有 $\sum_{i = 1}^{k - 1}w_i$，每项都减去该值，得到

调整前：$-s_k$, $w_k-s_{k + 1}$

调整后：$w_{k+1}-s_k$, $-s_{k+1}$

每项可以分别加上 $s_k+s_{k+1}$

调整前：$s_{k+1}$, $w_k+s_{k}$

调整后：$w_{k+1}+s_{k+1}$, $s_{k}$

现在我们比较 $\max \{ s_{k+1}, w_k+s_{k} \}$ 和 $\max \{ w_{k+1}+s_{k+1}$, $s_{k} \}$

因为 $s_k \le w_k + s_k$，$s_{k + 1} \le w_{k+1}+s_{k+1}$，所以两者的大小关系取决于 $w_k + s_k$ 与 $w_{k+1}+s_{k+1}$ 的大小关系，若前者大，交换后更优，若后者大，则交换前更优。

因此，对于序列的任意一个顺序，若出现了 $w_k + s_k > w_{k+1}+s_{k+1}$ 的情况，则交换两元素的位置，结果会更优。按照冒泡排序的知识，我们可以不断的按此规则进行交换，直到最终没有 $w_k + s_k > w_{k+1}+s_{k+1}$ 的情况出现，此时便是最优策略。

由上面的分析，本题将元素按照 $w_k + s_k$ 从小到大进行排序，便是最优解。

例3. Task

Task

今天某公司有 $M$ 个任务需要完成。每个任务都有相应的难度级别和完成任务所需时间。第 $i$ 个任务的难度级别为 $y_i$，完成任务所需时间为 $x_i$ 分钟。如果公司完成此任务，他们将获得（$500 \times x_i + 2 \times y_i$）美元收入。

该公司有 $N$ 台机器，每台机器都有最长工作时间和级别。如果任务所需时间超过机器的最长工作时间，则机器无法完成此任务。如果任务难度级别超过机器的级别，则机器无法完成此任务。每台机器一天内只能完成一项任务。每个任务只能由一台机器完成。

请为他们设计一个任务分配方案，使得该公司能够最大化他们今天可以完成的任务数量。如果有多种解决方案，他们希望选取赚取利润最高的那种。

在解决本题时，应该注意到收入为 $500x+2y$，并且 $0 < x < 1440, 0 \le y \le 100$。所以在考虑完成哪些任务时，需要优先考虑时间，即便一个任务时间和难度分别是$(x + 1, 0)$，另一个任务是 $(x, 100)$，如果只能二选一的话，依然应该选择第一个任务。

现在假设本题的任务和机器只考虑完成任务所需的时间。为了尽可能完成时间需求更多的任务，我们将任务按所需时间从多到少排序，机器按时间从多到少排序。

现在我们从 task1 开始为每个任务寻找合适的机器，如果 mac1 不能满足task1 的要求的话，那么所有的机器都不能满足 task1 的要求，这时候我们应该跳过 task1，为 task2 寻找合适的机器，而 mac1 还未使用，故我们需从 mac1 开始尝试，依此类推，现满足 task3 要求的机器有 mac1，mac2，mac3，这时我们应该选哪一个呢？都可以！随意选择哪个都可以得到最优的结果，考虑到我们的任务和机器顺序，能够满足 task3 要求的机器必能满足后面的任务。不过为了实现的方便，我们可以选择第一个满足 task3 要求的机器 mac1。接下来，对于 task4 来说，因为 mac1 已经选择，我们应从 mac2 开始尝试。

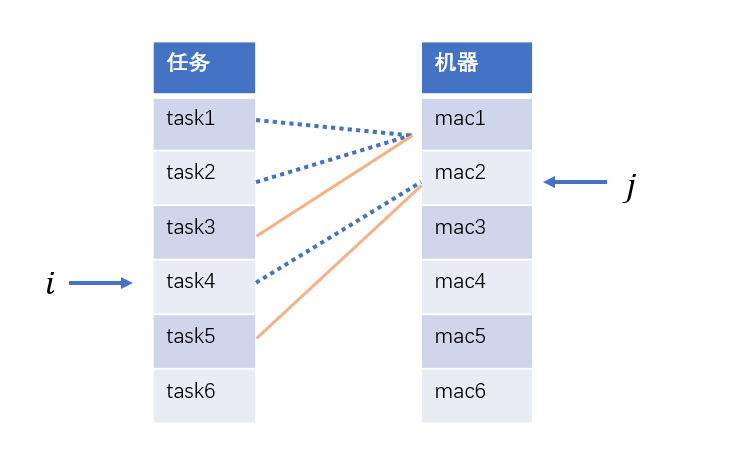
现在回到本题的限制，我们需要考虑的除了时间，还有难度，基于最开始的分析，我们需要尽可能完成所需时间更多的任务，如果时间一样，那么优先完成难度更大的任务，但机器怎么选择呢，自然，我们选择能够完成当前任务的机器中级别最低的那台，这样可以给后面的任务更多的选择。

现在的问题是，怎么实现呢？如果暴力的去寻找每个满足条件的机器，那么每次为每个任务匹配机器的时间复杂度为 $O(n)$，总时间复杂度为 $O(mn)$。

下面的图片中的 $(x，y)$ 分别表示时间和难度。

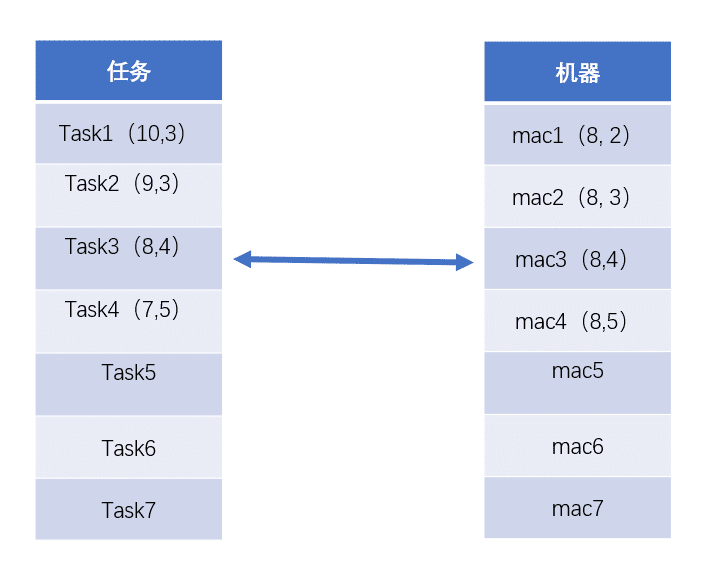对当前任务 task3 来说，mac3 和 mac4 可以满足条件，我们选择难度最低的 mac3 与之匹配。但是我们跳过的 mac1 和 mac2 依然可能是后面任务的最佳选择。

如何更快的找到匹配的机器呢，注意到本题特殊的数据范围，难度范围是 $0 \le y \le 100$。我们将所有的任务和机器按照时间从大到小排序，时间相同的话，难度从大到小排序。对于当前任务，我们按照难度分类统计所有满足时间要求，且还未使用过的机器数量，在这些机器中选择难度满足要求且最小的那一台与任务进行匹配，同时，该难度的机器的数量减少 1，剩下的机器工作时间也满足下一个任务的要求。这样，我们匹配的时间复杂度降到了 $O(100)$。总共的时间复杂度为 $O(100n)$，为 $10^8$ 这种级别，足够通过本题。

#include <bits/stdc++.h>
using namespace std;

#define tim first
#define dif second

const int N = 1e5 + 10;
int n, m;
pair<int, int> task[N], mac[N];
int cnt[105];

bool cmp(const pair<int, int> &a, const pair<int, int> &b) {
  if (a.tim != b.tim)  return a.tim > b.tim;
  return a.dif > b.dif;
}

void solve() {
  for (int i = 1; i <= n; i++) cin >> mac[i].tim >> mac[i].dif;
  for (int i = 1; i <= m; i++) cin >> task[i].tim >> task[i].dif;
  sort(mac + 1, mac + n + 1, cmp);
  sort(task + 1, task + m + 1, cmp);
  int tot = 0;
  long long ans = 0;
  for (int i = 1, j = 0; i <= m; i++) {
    while (j < n && mac[j + 1].tim >= task[i].tim) cnt[mac[++j].dif]++;
    for (int k = task[i].dif; k <= 100; k++) {
      if (cnt[k] == 0) continue;
      ans += task[i].tim * 500 + task[i].dif * 2;
      tot++;
      cnt[k]--;
      break;
    }
  }
  cout << tot << " " << ans << "\n";
}

int main() {
  while (cin >> n >> m) solve();
}